One Note to Bind Them All

I've been teaching about standing waves and their connection to music for years. But I recently discovered I haven't been making the connection explicit enough.  For instance, in a recent class when I remarked "See, that relationship between math and music is for real!", a student then responded "You mean the rhythm?"  But I was talking about pitch!

For standing waves:

Even though a note is identified by the fundamental frequency (the largest wave pictured above), it will have many higher harmonics buried within.  It is this distribution of higher harmonics (all obeying the mathematical relationship: Frequency of higher harmonic = N * Frequency of the fundamental), that give a musical note its timbre or unique sound.  It allows us to distinguish a middle A played on trumpet from the same note played on a piano.

Let's run some numbers.  If a string tuned to be a very low pitched "A" is plucked it will vibrate at all of the following frequencies:

N	Frequency
1	55
2	110
3	165
4	220
5	275
6	330
7	385
8	440
9	495
10	550

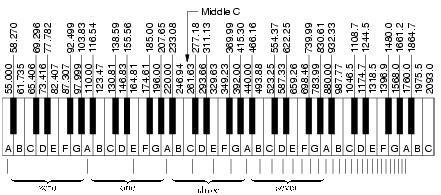
Compare this to the frequency of musical notes:

 Note that every octave is a frequency doubling.  So our low pitched A string actually contains all of the higher octaves within (N=2, N=4, N=8). What about the other harmonics? N=3, N= 6 are both the note "E".  A and E are perfect "fifths". Also, the N=5 is close to  C#.  Wait a sec!  A- C# - E; isn't that the A major chord??

Let's do another.  Take a string tuned to a low "C".  The first few harmonics would be:

N	Frequency
1	65.406
2	130.812
3	196.218
4	261.624
5	327.03
6	392.436
7	457.842
8	523.248
9	588.654
10	654.06

 N= 3 is a "G", N=5 is very close to "E"  C-E-G:  the classic C major chord!

The complete major chord is already contained within the first note and relationship between the musical notes is, just like everything in this universe, all about the physics!

Thanks to student KO for staying after and helping me investigate the perfect 5th relationship between the tuning fork held far from the ear and then close to the ear which led to this post.